Frank Pfenning originated the idea of refinement types in his seminal PLDI 1991 paper with Tim Freeman. Freeman and Pfenning’s refinement types allow programmers to work with refined datatypes, that is, sub-datatypes induced by refining the set of available constructors. For example, here’s what that looks like for lists, with a single refinement type, ? singleton:
datatype ? list = nil | cons of ? * ? list rectype ? singleton = cons ? nil
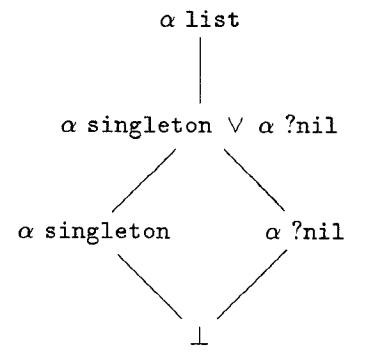
That is, a programmer defines a datatype ? list, but can identify refined types like ? singleton—lists with just one element. We can imagine a lattice of type refinements where ? list is at the top, but below it is the refinement of lists of length 0 or 1—written ? singleton ? ? nil. This type is itself refined by its constituent refinements, which are refined by the empty type. Here’s such a lattice, courtesy of a remarkably nice 1991-era TeX drawing:
Another way of phrasing all of this is that refinement types identify subsets of types. Back in 1983, Bengt Nordström and Kent Petersson introduced—as far as I know—the idea of subset types in a paper called Types and Specifications at the IFIP Congress. Unfortunately, I couldn’t find a copy of the paper, so it’s not clear where the notation {x:A|B(x)} set-builder-esque notation first came from, but it shows up in Bengt Nordström, Kent Petersson, and Jan M. Smith’s Programming in Martin-Löf’s Type Theory in 1990. Any earlier references would be appreciated. Update (2015-03-18): Colin Gordon pointed out that Robert Constable‘s Mathematics as programming from 1984 uses the subset type notation, as does the NUPRL tech report from 1983. The NUPRL TR came out in January ’83 while IFIP ’83 happened in September. Nate Foster, who works with Bob Constable, suspects that Constable has priority. Alright: subset types go to Robert Constable in January 1983 with the Nearly Ultimate Pearl. Going once…
My question is: when did we start calling {x:A | B(x)} and other similar subset types a “refinement type”? Any advice or pointers would be appreciated—I’ll update the post.
Susumu Hayashi in Logic of refinement types describes “ATTT”, which, according to the abstract, “has refi nement types which are intended to be subsets of ordinary types or specifications of programs”, where he builds up these refinements out of some set theoretic operators on singletons. By rights, this paper is probably the first to use “refinement type” to mean “subset type”… though I have some trouble pinpointing where the paper lives up to that claim in the abstract.
Ewen Denney was using refinement types to mean types and specifications augmented with logical propositions. This terminology shows up in his 1998 PhD thesis and his 1996 IFIP paper, Refinement Types for Specification.
In 1998, Hongwei Xi and Frank Pfenning opened the door to flexible interpretations of “refinements” in Eliminating Array Bound Checking Through Dependent Types. In Section 2.4, they use ‘refinement’ in a rather different sense:
Besides the built-in type families int, bool, and array, any user-defined data type may be refined by explicit declarations. …
typeref ? list of nat with nil <| ? list(0) | :: <| {n:nat} ? * ? list(n) -> ? list(n+1)
Later on, in Section 3.1, they have a similar use of the term:
In the standard basis we have refined the types of many common functions on integers such as addition, subtraction, multiplication, division, and the modulo operation. For instance,
+ <| {m:int} {n:int} int(m) * int(n) -> int(m+n)is declared in the system. The code in Figure 3 is an implementation of binary search through an array. As before, we assume:
sub <| {n:nat} {i:nat | i < n} ? array(n) * int(i) -> ?
So indices allow users to refine types, though they aren’t quite refinement types. In 1999, Xi and Pfenning make a strong distinction in Dependent Types in Practical Programming; from Section 9:
…while refinement types incorporate intersection and can thus ascribe multiple types to terms in a uniform way, dependent types can express properties such as “these two argument lists have the same length” which are not recognizable by tree automata (the basis for type refinements).
Now, throughout the paper they do things like “refine the datatype with type index objects” and “refine the built-in types: (a) for every integer n, int(n) is a singleton type which contains only n, and (b) for every natural number n, 0 a array(n) is the type of arrays of size n”. So here there’s a distinction between “refinement types”—the Freeman and Pfenning discipline—and a “refined type”, which is a subset of a type indicated by some kind of predicate and curly braces.
Jana Dunfield published a tech report in 2002, Combining Two Forms of Type Refinements, where she makes an impeccably clear distinction:
… the datasort refinements (often called refinement types) of Freeman, Davies, and Pfenning, and the index refinements of Xi and Pfenning. Both systems refine the simple types of Hindley-Milner type systems.
In her 2004 paper with Frank, Tridirectional Typechecking, she maintains the distinction between refinements, but uses a term I quite like—“property types”, i.e., types that guarantee certain properties.
Yitzhak Mandelbaum, my current supervisor David Walker, and Bob Harper wrote An Effective Theory of Type Refinements in 2003, but they didn’t quite have subset types. Their discussion of related work makes it seem that they interpret refinement types as just about any device that allows programmers to use the existing types of a language more precisely:
Our initial inspiration for this project was derived from work on refinement types by Davies and Pfenning and Denney and the practical dependent types proposed by Xi and Pfenning. Each of these authors proposed to sophisticated type systems that are able to specify many program properties well beyond the range of conventional type systems such as those for Java or ML.
In the fairly related and woefully undercited 2004 paper, Dynamic Typing with Dependent Types, Xinming Ou, Gang Tan, Yitzhak Mandelbaum, and David Walker used the term “set type” to define {x:A | B(x)}.
Cormac Flanagan‘s Hybrid Type Checking in 2006 is probably the final blow for any distinction between datasort refinements and index refinements: right there on page 3, giving the syntax for types, he writes “{x:B|t} refinement type“. He says on the same page, at the beginning of Section 2, “Our refinement types are inspired by prior work on decidable refinement type systems”, citing quite a bit of the literature: Mandelbaum, Walker, and Harper; Freeman and Pfenning; Davies and Pfenning ICFP 2000; Xi and Pfenning 1999; Xi LICS 2000; and Ou, Tan, Mandelbaum, and Walker. After Cormac, everyone just seems to call them refinement types: Ranjit Jhala‘s Liquid Types, Robby Findler and Phil Wadler in Well typed programs can’t be blame, my own work, Andy Gordon in Semantic Subtyping with an SMT Solver. This isn’t a bad thing, but perhaps we can be more careful with names. Now that we’re all in the habit of calling them refinements, I quite like “indexed refinements” as a distinction. Alternatively, “subset types” are a very clear term with solid grounding in the literature.
Finally: I didn’t cite it in this discussion, but Rowan Davies‘s thesis, Practical Refinement-Type Checking, was extremely helpful in looking through the literature.
Edited to add: thanks to Ben Greenman for some fixes to broken links and to Lindsey Kuper and Ron Garcia for helping me clarify what refines what.
2020-04-27 update: Shriram Krishnamurthi suggests that Robert (Corky) Cartwright had a notion of “refinement type” in “User-Defined Data Types as an Aid to Verifying LISP Programs” from ICALP 1976 and with John McCarthy in First order programming logic in POPL 1979. I haven’t been able to get a PDF copy of the ICALP paper (please send me one if you can find it!). The POPL paper is clearly related:
The key idea underlying our formal systems is that recursive definitions of partial functions can be interpreted as equations extending a first order theory of the program domain.
Their model is typed, and the paper is about how Corky and John independently discovered ways of addressing recursion/fixed points. They translate programs to logic, treating checks in negative positions as ?‚ like Blume and McAllester’s “A sound (and complete) model of contracts”, but they don’t seem to think of themselves as actually refining types per se. This paper is an interesting early use of an SMT-like logic to prove properties of programs… though they do the proofs by hand!
Cartwright’s dissertation, A Practical Formal Semantic Definition and Verification System for Typed Lisp (which I’ve hosted here, since I could only find it on a very slow server elsewhere) makes it clear that the work is indeed very closely related. Here’s a long quote from the end of his introduction:
The auxiliary function ATOMLIST [a program predicate] serves as a clumsy mechanism for specifying the implicit data type atom-list [which he defined by hand]. If we included atom-list as a distinct, explicit data type in our programming language and expanded our first-order theory to include atom-lists as well as S-expressions, the informal proof using induction on atom-lists [given earlier] could be formalized directly in our first order system. However, since LISP programs typically involve a wide variety of abstract data types, simply adding a few extra data types such as atom-list to LISP will not eliminate the confusion caused by dealing with abstract data type representations rather than the abstract types themselves. In fact, the more complex that an abstract type is, the more confusing that proofs involving its representations are likely to be. Consequently, I decided that the best solution to this problem is to include a comprehensive data type definition facility in LISP and to formally define the semantics of a program P by creating a first-order theory for the particular data types defined in P. The resulting language TYPED LISP is described in the next chapter.