In hybrid type checking, a subtyping relationship between subset types {x:T|e} determines when it’s safe to omit a cast. The structural extension of subtyping to, e.g., function types, gives us a straightforward way to achieve verification by optimization: if we can prove that a cast is from a subtype to a supertype, there’s no need to pay the runtime cost of checking anything.

When should we reject a hybrid typed program? In Flanagan’s seminal paper, he offers a straightforward plan:

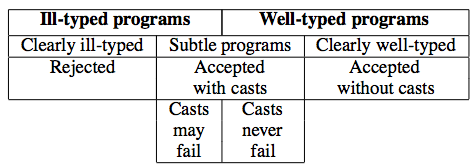
Flanagan enacts this plan by rejecting casts which are provably not from a subtype to a supertype: if the SMT solver finds that a cast might fail, then it rejects the program. In his model of an SMT solver, returning a checkmark (✓) when checking proves subtyping, a question mark (?) when checking times out, or an x-mark (×) when a counterexample of subtyping is found.

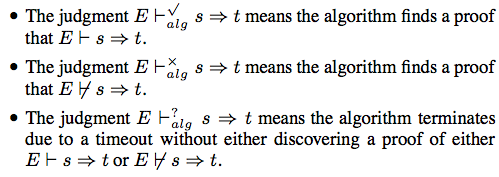
The compilation and checking judgment (a/k/a cast insertion) will insert a cast on successful or indeterminate checking, but has no rules for (and therefore rejects) programs where there is a counterexample.

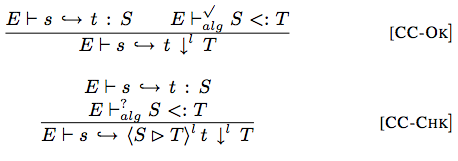
Unfortunately, such a policy is too restrictive. For example, an SMT solver can easily prove that {x:Int|true} doesn’t imply {x:Int|even x}… but such a program shouldn’t be rejected! We should only reject programs that must fail.

When must a cast fail? When the two types are disjoint, i.e., when they don’t share any values. Since our language with casts has when the only normal form typeable at both types is an error. Cătălin HriÅ£cu got a good start on this in his thesis (see sections 2.4.6 and the end of 3.4.4), where he defines a notion of non-disjointness. He doesn’t define the notion for function types, but that’s actually very easy: so long as two function types are compatible (i.e., equal after erasure of refinements), they are non-disjoint. Why? Well, there’s at least one value that {x:T|e11}→{x:T|e12} and {x:T|e21}→{x:T|e22} have in common: λx. blame.

I can imagine a slightly stronger version: if the domain type is a refinement of base type, then we could exclude functions which could never even be called, i.e., with disjoint domains. At higher orders, though, there’s no way to tell (maybe the function in question never calls its argument), so I think the more liberal interpretation is the right starting point.

NB I briefly discuss when to reject hybrid-typed programs in my dissertation (Section 6.1.4).